Deriving the modified Breguet range equation for a hybrid-turboelectric aircraft

Summary

• Modifications to the Breguet range equation considering hybridization of energy storage are proposed
• Payload-range charts are constructed to illustrate the impact of hybridization on airplane performance for a TBM 700-sized design using two different non-dimensionalizations
• Simple, analytical expressions for the impact of technology and mission requirements on airplane weight are derived and explained

Motivation

With recent progress in hybrid-electric propulsion systems components, I want to get a jump start on one of my main research tasks, which will be to develop a "Common Research Model" of an electric and hybrid-electric aircraft powertrain. There are several groups of researchers using their own tools in aircraft design research right now. The models mostly fall into one of two categories:

• Low-fidelity, equation-based methods (fully disclosed in each paper)
• Medium- or high- fidelity proprietary models (not publicly available)

The second case causes problems for anyone who would like to compare the results of different research groups, different hybrid-electric architectures, and so on in an apples-to-apples fashion.

My goal is to develop a model that is:

• Open-source
• Not export controlled
• Extensible for all conceivable system architectures (series-hybrid, parallel-hybrid, fully electric, etc.)
• Object-oriented with inheritance (in Python)
• Modular and able to wrap industry-standard or non-open source tools (such as NPSS)
• Time- and state- dependent
• Responsive to changes in geometry and system connectivity

and has:

• A library of standard powertrain component models (for running reference cases)
• At least the following state variables: energy, power, system voltage, current, heat
• Integrated weight and mass properties (including weight as a function of rated power, energy, etc)
• Elegant support for technology level sensitivity studies (such as parametrically varying specific energy or power)

The range equation for a fully electric airplane

As I conduct a literature search in the state of the art of electric aircraft modeling, I wanted to bracket the low-fidelity end of the spectrum and determine the roughest possible way of approaching the problem. The Breguet Range Equation is sort of the equivalent mission analysis tool for conventional aircraft with liquid fuel. It elegantly illustrates how top level aircraft design parameters (such as the lift-to-drag ratio, specific fuel consumption, and weights) work together to dictate the range of an aircraft.

The Breguet Range Equation does not apply to electric aircraft because their weight does not change as energy is used. Therefore, I used the power-balance approach that the BRE is derived from and modified it for constant weight. This is a pretty trivial task.

$$R_{elec}=\frac{c_b}{g} \frac{C_L}{C_D} \frac{W_{batt}}{W_{TO}} \eta_i\eta_m\eta_p$$

Where:

• \(\frac{C_L}{C_D}\) is the lift to drag ratio
• \(c_b\) is the battery specific energy (energy / mass)
• \(W_{batt}, W_{TO}\) are the battery weight, takeoff weight
• \(\eta_i, \eta_m, \eta_p\) are the inverter, motor, and propulsive efficiency
• \(g\) is the gravitational constant

Modifications for hybrid-electric aircraft

Next, I considered a hybrid-electric aircraft where power is supplied exclusively by electricity but power is generated by either a turbine with generator or a battery pack. Because the drag is minimized when weight is minimized, the range of the aircraft will always be greatest when the fuel is used before battery power (Unused reserve fuel may mean that this approach doesn't minimize CO2 emissions, however). The mix of fuel and battery weight carried on each mission will depend on the target range and the payload required; some missions will be infeasible given the design of the airplane and the performance of the fuel and batteries . We need to introduce a couple more parameters:

• \(\eta_g\) is the generator efficiency
• \(c_p\) is the shaft power specific fuel consumption

I wondered about ways to non-dimensionalize the problem a little bit to gain some general insight:

• Let \(f_{ew}\) be the empty weight fraction: \(\frac{W_e}{ MTOW}\). This parameter is primarily a function of the technology level of the airplane (better technology such as carbon composite structure = lower \(f_{ew}\))

• Let ϕ be the battery fraction: the percentage of useful load made up of battery weight. In other words: W_batt = \(\phi (1-f_{ew})\) MTOW
• Let ψ be the fuel fraction: the percentage of useful load occupied by fuel weight.

An alternative method is to non-dimensionalize by total energy. A Bauhaus Luftfahrt paper was my inspiration for this approach [1].

• Let ε be the degree of energy hybridization: the percentage of total energy used during the mission sourced from battery power. ε = 1 is a fully-electric mission.

It turns out that weight completely drops out of the range equation and MTOW shows up only in the equation for payload.

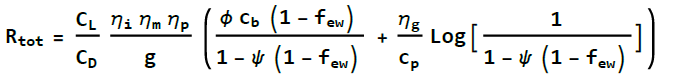
To illustrate what this can tell us about performance and mission planning of hybrid-electric aircraft, I created a test case similar to the SOCATA TBM 700, a single-engine turboprop carrying up to 6 people, with a max range of 3400km. You can view my assumptions and source code here. Of note, I assumed 400 W*hr/kg specific energy for the battery pack.

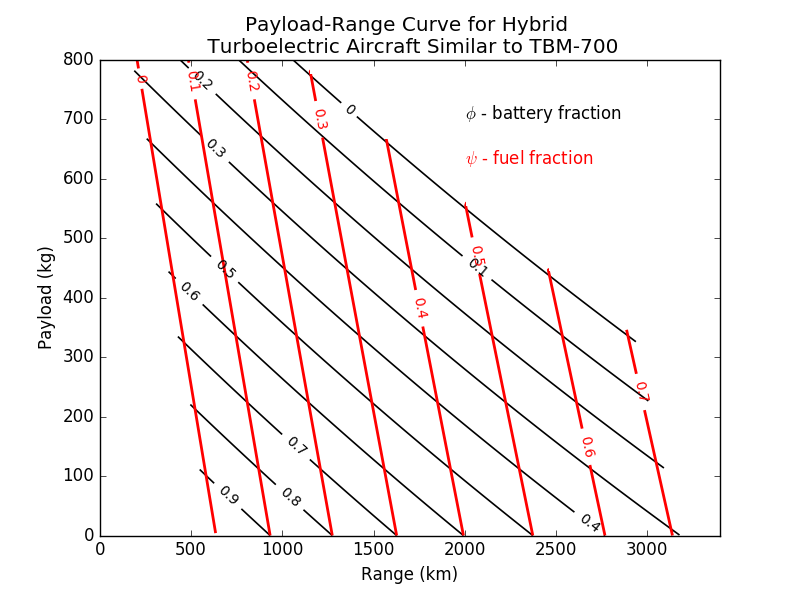
This is an example of a payload-range curve. Normally, a payload-range curve is a simple outline demonstrating the maximum payload that can be carried for a given range, limited by various design factors including:

• the maximum zero-fuel weight (MZFW, the top-left line)
• maximum takeoff weight (MTOW, the diagonal line)
• maximum fuel volume (the right line)

I also inverted the axes, plotting fuel fraction and battery fraction in the rectangular frame, with payload and range as the third and fourth variables. In an aircraft where batteries and fuel were equally efficient at providing range per unit added weight, the black and red lines would be parallel.

One-variable parameterization

As a reminder, ε represents the percentage of total mission energy provided by batteries. This method gave better insight into the design problem graphically, but the equations were a little more convoluted. This is the expression for total range:

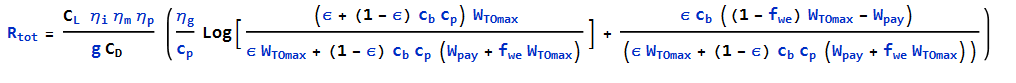
The reason I like this parameterization is that it reflects the real aircraft design process more closely. Generally, a design team will have a payload-range target in mind (for example: 800kg payload over 2000km range) and the overall sizing of the airplane falls out of the analysis. The one-variable method allows us to look at the impact of hybridization on the maximum takeoff weight (MTOW) of the airplane, which is important because MTOW is a key indicator of complexity and cost.

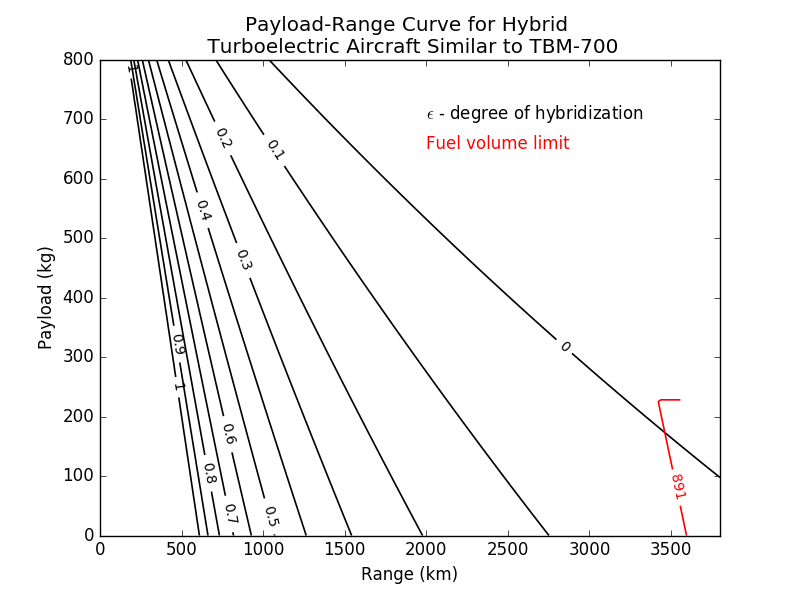
I like this plot (source) better than the two-parameter version. There is a single contour variable (instead of having to find intersections of two variables) which directly illustrates the impact of hybridization. The maximum fuel volume constraint is simply shown in kg rather than a weight fraction (which is why it looks slightly different in that region compared to the plot above).

This plot clearly illustrates that fuel works extremely effectively as a "range-extender" due to its high specific energy and the fact that the airplane loses weight (and therefore, drag) as it loses fuel. The aircraft can barely fly 500km on battery power alone, even with just a pilot and no useful payload. It also demonstrates that the "challenge" of hybridization is nonlinear: small degrees of hybridization are possible at useful ranges.

Insight into the electric aircraft design problem

If we set ε=1 we obtain the fully-electric case. Solving the range equation for MTOW, we obtain: $$W_b=\frac{(1-\epsilon)c_bc_p((1-f_{we})W_{TOmax}-W_{pay})}{\epsilon+(1-\epsilon) c_b c_p}$$

As intuition would tell us, the MTOW depends linearly on the target payload, and inversely with range and empty weight fraction. Taking a couple of derivatives gives us some additional insight into the electric aircraft design problem. We are interested in how the weight (~cost) of an aircraft depends on the specific energy (energy mass density) of the battery, which is falling over time. We also care about the "cost" of increasing the range requirement of an aircraft (longer range aircraft need to be heavier). Those expressions are as follows: $$\frac{dW_{TOmax}}{dc_b} = -\frac{R W_{pay}}{c_b K_e}$$ $$\frac{dW_{TOmax}}{dR} = \frac{W_{pay}}{K_e}$$

The first expression tells us how weight decreases (good) when battery specific energy increases (good). The savings are proportional to both range and payload - so long range airplanes benefit proportionally more than short range ones from improvements in battery technology.

Note that \(c_b^2\) appears in the denominator (once \(K_e\) is substituted) indicating that improvements in battery technology will have strongly diminishing returns over time. I will explore the implications of this more in a subsequent post.

The second expression tells us that the rate of MTOW increase with each increment in range is proportional to the payload.

Intriguingly, there is a term that appears identically in the denominator of both expressions, which I will call \(K_e\). $$K_e=\frac{c_b}{g} \frac{C_L}{C_D} \eta_i \eta_m \eta_p (1-f_{we}-\frac{gR}{c_b\frac{C_L}{C_D}\eta_i\eta_m\eta_p})^2$$

\(K_e\) is not really a constant because it depends on range, but it's a great summary of how all the technology and design levers play together in electric aircraft. We want this number to be LARGE because it means we get to fly farther in lighter, cheaper airplanes.

Note that there is a singular point at \( (1-f_{we}-\frac{gR}{c_b\frac{C_L}{C_D}\eta_i\eta_m\eta_p})=0\). More on this later - it represents the relationship for the upper limit on range for a given battery \(c_b\), or conversely, the lower limit on \(c_b\) for a given range. The economic limit will be 20-40% offset from the singularity.

Edit: I later discovered that I independently derived an expression published in [2].

Summary

As far as I know, this is the first time that payload-range charts have been created with a fuel/battery mix as an input parameter although it is possible I just haven't encountered it yet in the literature.

This was a fun exercise and it provides a lower limit on the sophistication required to derive some insights into the hybrid-electric aircraft design problem. The doubly-bad impact of range on electric aircraft MTOW illustrates why companies like Zunum are focusing on shorter-range missions; though a breakthrough in battery specific energy would change the picture significantly.

[1] Isikveren, A. T., Kaiser, S., Pornet, C., & Vratny, P. C. (2014). Pre-design strategies and sizing techniques for dual-energy aircraft. Aircraft Engineering and Aerospace Technology, 86(6), 525–542. https://doi.org/10.1108/AEAT-08-2014-0122

[2] Hepperele, M. (2012) Electric Flight - Potential and Limitations. NATO Report STO-MP-AVT-209.